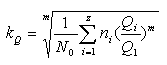不稳定变应力可分为非规律性的和规律性的两大类。

　　一、非规律性的不稳定变应力：其变应力参数的变化要受到很多偶然因素的影响，是随机地变化的。承受非规律的不稳定变应力的典型零件，以汽车的钢板弹簧为例。作用在它上面的载荷和应力的大小，要受到载重量大小、行车速度、轮胎充气程度、路面状况以及驾驶员的技术水平等一系列因素的影响。对于这一类的问题，应根据大量的试验，求得载荷及应力的统计分布规律，然后用统计疲劳强度的方法来处理。

　　二、规律性的不稳定变应力：其变应力参数的变化有一个简单的规律。承受近似于规律性的不稳定变应力的零件，以专用机床的主轴、高炉上料机构的零件为例。对于这一类问题，是根据疲劳损伤累计假说进行计算的。

　　下面左图为一规律性的不稳定变应力的示意图。变应力σ1（对称循环变应力的最大应力，或不对称循环变应力的等效对称循环变应力的应力幅，以下同此）作用了n1次，σ2作用了n2次，……。把左图所示的应力图放在材料的σr－Ｎ坐标上，如下面右图所示。根据σr－Ｎ曲线，可以找出仅有σ1作用时使材料发生疲劳破坏的应力循环次数N1。假使应力每循环一次都对材料的破坏起相同的作用，则应力σ1每循环一次对材料的损伤率即为1/N1，而循环了n1次的σ1对材料的损伤率即为n1/N1。如此类推，循环了n2次的σ2对材料的损伤率即为n2/N2，……。

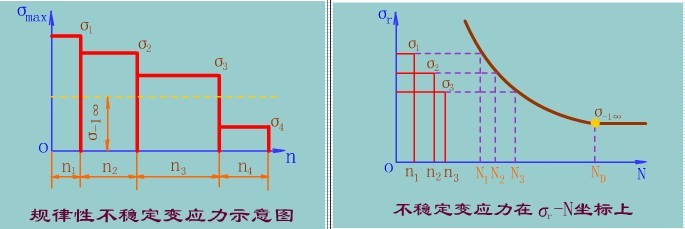
　　按上面左图所示，如σ4小于材料的持久疲劳极限σ-1∞,它当然可以作用无限多次循环而不引起疲劳破坏。这就是说，小于材料持久疲劳极限的工作应力对材料不起疲劳损伤的作用，故在计算时可以不予考虑。

　　因为当损伤率达到100%时，材料即发生疲劳破坏，故对应于极限状况有

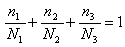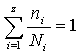一般地写成 上式是疲劳损伤累积假说的数学表达式。试验证明，当各个作用的应力幅无巨大的差别以及无短时的强烈过载时，这个规律是正确的；当各级应力是先作用最大的，然后依次降低时，上式的等号右边将不等于1而小于1；当各级应力是先作用最小的，然后依次升高时，则上式等号右边要大于1。通过大量的试验，可以有以下的关系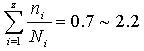： 当上式右边的值小于1时，表示每一循环的变应力的损伤率实际上是大于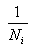的。这一现象可以解释为：使初始疲劳裂纹产生和使裂纹扩展所需的应力水平是不同的。递升的变应力不易产生破坏，是由于前面施加的较小的应力对材料不但没有使初始疲劳裂纹产生，而且对材料起了强化的作用；递减的变应力却由于开始作用了最大的变应力，引起了初始裂纹，则以后施加的应力虽然较小，但仍能够使裂纹扩展，故对材料有削弱的作用，因此使上式右边的值小于1。虽然如此，由于疲劳试验的数据具有很大的离散性，从平均的意义上说，在设计中应用公式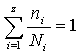还是可以得出一个较为合理的结果的。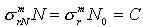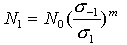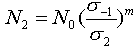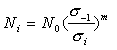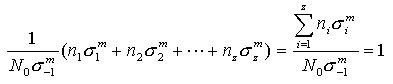 根据公式 可得： ；；… ； 把它们代入公式：，即得到不稳定变应力时的极限条件为： 如果材料在上述应力作用下还未达到破坏，则 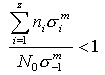或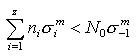 如以σ1作为计算时所采用的应力值，则上式变为 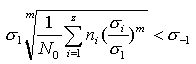上式左边根号部分表示了变应力参数的变化情况。令 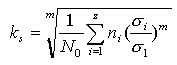ks称为应力情况系数。引入ks后，计算安全参数Sca及强度条件则为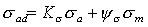 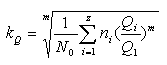对于不对称循环的不稳定变应力，可先按公式求出各等效的对称循环变应力σad1、σad2、…，然后应用上面两式进行计算。 如果把载荷作为参数来进行计算，则对应于应力情况系数，可以定义一个载荷情况系数kQ，它等于